Skip to content

1.17. 神经网络模型（有监督）

警告

此实现不适用于大规模应用程序。特别是，scikit-learn没有提供GPU支持。要获得更快、基于GPU的实现，以及提供更多灵活性以构建深度学习体系结构的框架，请参见相关项目。

1.17.1. 多层感知器

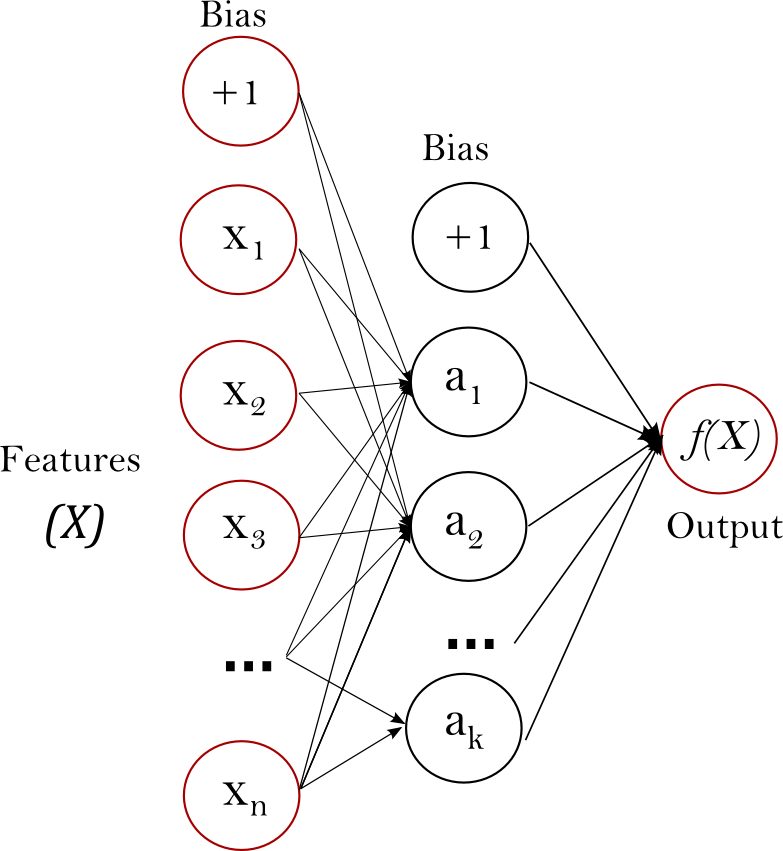
多层感知器 (MLP)是一种有监督的学习算法，它通过在数据集进行训练来学习函数$f(\cdot):R^m \rightarrow R^o$，其中$m$是输入的维数，$o$是输出的维数。给定一组特征$X = {x_1, x_2, ..., x_m}$一个标签$y$，它可以学习用于分类或回归的非线性函数。它不同于logistic回归，在输入层和输出层之间可以有一个或多个非线性层，称为隐藏层。图1显示了一个带有标量输出的单隐藏层MLP。

https://scikit-learn.org/stable/_images/multilayerperceptron_network.png

图 1 : 一个隐藏层的MLP.

最左边的层称为输入层，由一组代表输入特征的神经元$\{x_i | x_1, x_2, ..., x_m\}$组成。隐藏层中的每个神经元用加权线性和$w_1x_1 + w_2x_2 + ... + w_mx_m$变换前一层的值，然后再通过非线性激活函数$g(\cdot):R \rightarrow R$进行变换，如双曲正切函数(tanh)。输出层从最后一个隐藏层接收值并将其转换为输出值。

模块包含公共属性coefs_ 和 intercepts_。coefs_是一个权重矩阵列表，其中下标为$i$的权重矩阵表示第$i$层和第$i+1$层之间的权重。intercepts_是一个偏移向量，其中下标为$i$的向量表示添加到第$i+1$层的偏移值。

多层感知器的优点是：

  • 能够学习非线性模型
  • 能够使用partial_fit学到实时(real-time)模型

多层感知器（MLP）的缺点包括：

  • 具有隐藏层的MLP具有非凸损失函数，其存在多个局部极小值。因此，不同的随机权重初始化会导致不同的验证精度。
  • MLP需要调整许多超参数，例如隐藏层神经元的数量、层数和迭代次数。
  • MLP对特征缩放很敏感。

请参阅实用小贴士一节，以解决其中的一些缺点。

1.17.2. 分类

类MLPClassifier实现了一个多层感知器（MLP）算法，该算法使用Backpropagation进行训练。

MLP在两个数组上进行训练：大小为(n_samples，n_features)的数组X，它保存浮点型特征向量的训练样本；大小为(n_samples)的数组y，它保存训练样本的目标值（类标签）： 

>>> from sklearn.neural_network import MLPClassifier
>>> X = [[0., 0.], [1., 1.]]
>>> y = [0, 1]
>>> clf = MLPClassifier(solver='lbfgs', alpha=1e-5,
...                     hidden_layer_sizes=(5, 2), random_state=1)
...
>>> clf.fit(X, y)
MLPClassifier(alpha=1e-05, hidden_layer_sizes=(5, 2), random_state=1,
              solver='lbfgs')

经过拟合（训练），模型可以预测新样本的标签：

>>> clf.predict([[2., 2.], [-1., -2.]])
array([1, 0])

MLP可以为训练数据拟合一个非线性模型。clf.coefs_包含构成模型参数的权重矩阵：

>>> [coef.shape for coef in clf.coefs_]
[(2, 5), (5, 2), (2, 1)]

目前，MLPClassifier 只支持交叉熵损失函数，它允许通过运行predict_proba方法进行概率估计。

MLP使用反向传播进行模型训练。更准确地说，它使用梯度下降来训练，而梯度是用反向传播来计算的。对于分类，它最小化了交叉熵损失函数，给出了每个样本$x$的概率估计向量$P（y | x）$：

>>> clf.predict_proba([[2., 2.], [1., 2.]])
array([[1.967...e-04, 9.998...-01],
       [1.967...e-04, 9.998...-01]])

MLPClassifier通过将Softmax作为输出函数来支持多分类。

此外，该模型支持多标签分类，一个样本可以属于多个类。对于每个类，原始输出通过logistic函数进行变换。大于或等于“0.5”的值舍入为“1”，否则舍入为“0”。对于样本的预测输出，值为“1”的索引表示该样本的预测类别。

>>> X = [[0., 0.], [1., 1.]]
>>> y = [[0, 1], [1, 1]]
>>> clf = MLPClassifier(solver='lbfgs', alpha=1e-5,
...                     hidden_layer_sizes=(15,), random_state=1)
...
>>> clf.fit(X, y)
MLPClassifier(alpha=1e-05, hidden_layer_sizes=(15,), random_state=1,
              solver='lbfgs')
>>> clf.predict([[1., 2.]])
array([[1, 1]])
>>> clf.predict([[0., 0.]])
array([[0, 1]])

有关详细信息，请参见下面的案例和MLPClassifier.fit的文档。

案例:

1.17.3. 回归

类MLPRegressor实现了一个多层感知器（MLP），该感知器使用反向传播进行训练，但在输出层中没有使用激活函数，这也可以看作使用标识函数(identity function)作为激活函数。因此，它使用平方误差作为损失函数，输出是一组连续值。

MLPRegressor 还支持多输出回归，其中一个样本可以有多个目标值。

1.17.4. 正则化

MLPRegressor和MLPClassifier都使用参数alpha作为正则化（L2正则化）项，这有助于通过惩罚值较大的权重以避免过拟合。下图显示了不同 alpha 值下决策函数的变换。

https://scikit-learn.org/stable/_images/sphx_glr_plot_mlp_alpha_0011.png

有关更多信息，请参见下面的案例。

案例：

1.17.5. 算法

MLP使用Stochastic Gradient Descent, Adam,或 L-BFGS进行训练

随机梯度下降（SGD）利用损失函数的梯度来更新需要调整的参数，即 $$ w \leftarrow w - \eta (\alpha \frac{\partial R(w)}{\partial w} + \frac{\partial Loss}{\partial w}) $$ 其中$\eta$是参数空间搜索中控制步长的学习率。$Loss$是网络的损失函数。

更多细节可在SGD文档中找到。

Adam在某种意义上类似于SGD，它是一个随机优化器(stochastic optimizer)，但它可以根据低阶矩的自适应估计自动调整更新参数的量。

通过SGD或Adam，训练支持在线和小批量学习(online and mini-batch learning)模式。

L-BFGS是一个近似Hessian矩阵的求解器，其中，Hessian矩阵表示函数的二阶偏导数。此外，L-BFGS近似Hessian矩阵的逆矩阵以进行参数更新。实现使用了L-BFGS的Scipy版本。

如果选择的求解器是“L-BFGS”，则训练不支持在线或小批量学习模式。

1.17.6. 复杂度

假设有$n$个训练样本、$m$个特征、$k$个隐藏层，每个隐藏层包含$h$个神经元（为了简单起见）和$o$个输出神经元。反向传播的时间复杂度为$O(n\cdot m \cdot h^k \cdot o \cdot i)$，其中$i$是迭代次数。由于反向传播具有很高的时间复杂度，建议从较少的隐神经元和较少的隐层开始训练。

1.17.7. 数学公式

给出了一组训练示例$(x_1, y_1), (x_2, y_2), \ldots, (x_n,y_n)$，其中$x_i \in \mathbf{R}^n$和$y_i \in \{0, 1\}$，单隐层单神经元MLP学习到的函数是$f(x) = W_2 g(W_1^T x + b_1) + b_2$，其中 $W_1 \in \mathbf{R}^m$和$W_2, b_1, b_2 \in \mathbf{R}$是模型参数。 $W_1$, $W_2$分别表示输入层与隐藏层之间和隐藏层与输出层之间的权重；$b_1$,$ b_2$分别表示添加到隐藏层和输出层的偏移值。$g(\cdot) : R \rightarrow R$是激活函数，默认设置为双曲正切函数tanh。写为， $$ g(z)= \frac{e^z-e^{-z}}{e^z+e^{-z}} $$ 对于二分类，$f(x)$通过logistic函数$g(z)=1/(1+e^{-z})$获得0到1之间的输出值。阈值设置为0.5，将大于或等于0.5的输出样本分配给正类，其余的分配给负类。

如果有两个以上的类，那么$f(x)$本身就是一个大小(n_classes,)的向量。它不是通过logistic函数，而是通过softmax函数进行变换，写为， $$ \text{softmax}(z)i = \frac{\exp(z_i)}{\sum{l=1}^k\exp(z_l)} $$ 其中 $z_i$表示softmax函数的第$i$个输入元素，它对应于第$i$类，$K$是类别数量。结果是由样本$x$属于每个类的概率组成的向量。最终的输出是概率最高的类。

在回归问题中，输出为 $f(x)$；因此，输出激活函数只是身份函数(identity function)。

MLP根据问题类型使用不同的损失函数。分类使用交叉熵作为损失函数，在二分类情况下，损失函数为， $$ Loss(\hat{y},y,W) = -y \ln {\hat{y}} - (1-y) \ln{(1-\hat{y})} + \alpha ||W||_2^2 $$ 其中$\alpha ||W||_2^2$是惩罚复杂模型的L2正则化项（aka惩罚）； $\alpha > 0$是控制惩罚大小的非负超参数。

对于回归问题，MLP使用平方误差损失函数；写为， $$ Loss(\hat{y},y,W) = \frac{1}{2}||\hat{y} - y ||_2^2 + \frac{\alpha}{2} ||W||_2^2 $$ 从初始随机权值出发，多层感知器（multi-layer perceptron，MLP）通过反复更新这些权值来最小化损失函数。在计算损失后，反向传播将其从输出层传播到前面个层，更新每个权重参数以减少损失(loss)。

在梯度下降中，计算损失函数相对于权重的梯度$\nabla Loss_{W}$，并从 $W$中扣除。更为正式的说法是， $$ W^{i+1} = W^i - \epsilon \nabla {Loss}_{W}^{i} $$ 其中，$i$是迭代步数，$\epsilon$是值大于0的学习率。

当达到预设的最大迭代次数时，或者当损失值低于某个特定的小数值时，算法停止。

1.17.8. 实用小贴士

  • 多层感知器对特征缩放敏感，因此强烈建议将数据进行归一化。例如，将输入向量X上的每个属性缩放为[0，1]或[-1，+1]，或将其标准化为平均值0和方差1。请注意，必须对测试集应用相同的缩放比例才能获得有意义的结果。可以使用 StandardScaler进行标准化。
   >>> from sklearn.preprocessing import StandardScaler  # doctest: +SKIP
   >>> scaler = StandardScaler()  # doctest: +SKIP
   >>> # 不要作弊-只在训练数据集上进行拟合
   >>> scaler.fit(X_train)  # doctest: +SKIP
   >>> X_train = scaler.transform(X_train)  # doctest: +SKIP
   >>> # 对测试数据应用相同的转换
   >>> X_test = scaler.transform(X_test)  # doctest: +SKIP

另一种推荐的方法是在Pipeline中使用 StandardScaler

  • 最好使用GridSearchCV找到一个合理的正则化参数$\alpha$，通常在 10.0 ** -np.arange(1, 7)范围内。

  • 根据经验，我们观察到L-BFGS收敛更快，且在小数据集上具有更好的解。然而，对于相对较大的数据集，Adam鲁棒性强。它通常收敛得很快，性能也很好。另一方面，如果学习速率得到正确的调整，使用带momentum 或 nesterov’s momentum的SGD算法可以比这两种算法有更好的性能。

1.17.9. 使用 warm_start 进行更多控制

如果您希望对SGD中的停止条件或学习率进行更多控制，或希望进行其他监视，请使用warm_start=True 和 max_iter=1 并自行迭代可能会有所帮助：

>>> X = [[0., 0.], [1., 1.]]
>>> y = [0, 1]
>>> clf = MLPClassifier(hidden_layer_sizes=(15,), random_state=1, max_iter=1, warm_start=True)
>>> for i in range(10):
...     clf.fit(X, y)
...     # additional monitoring / inspection
MLPClassifier(...

参考文献:

(C) 2007 - 2019, scikit-learn 开发人员 (BSD 许可证). 此页显示源码